20 Questions on Sets

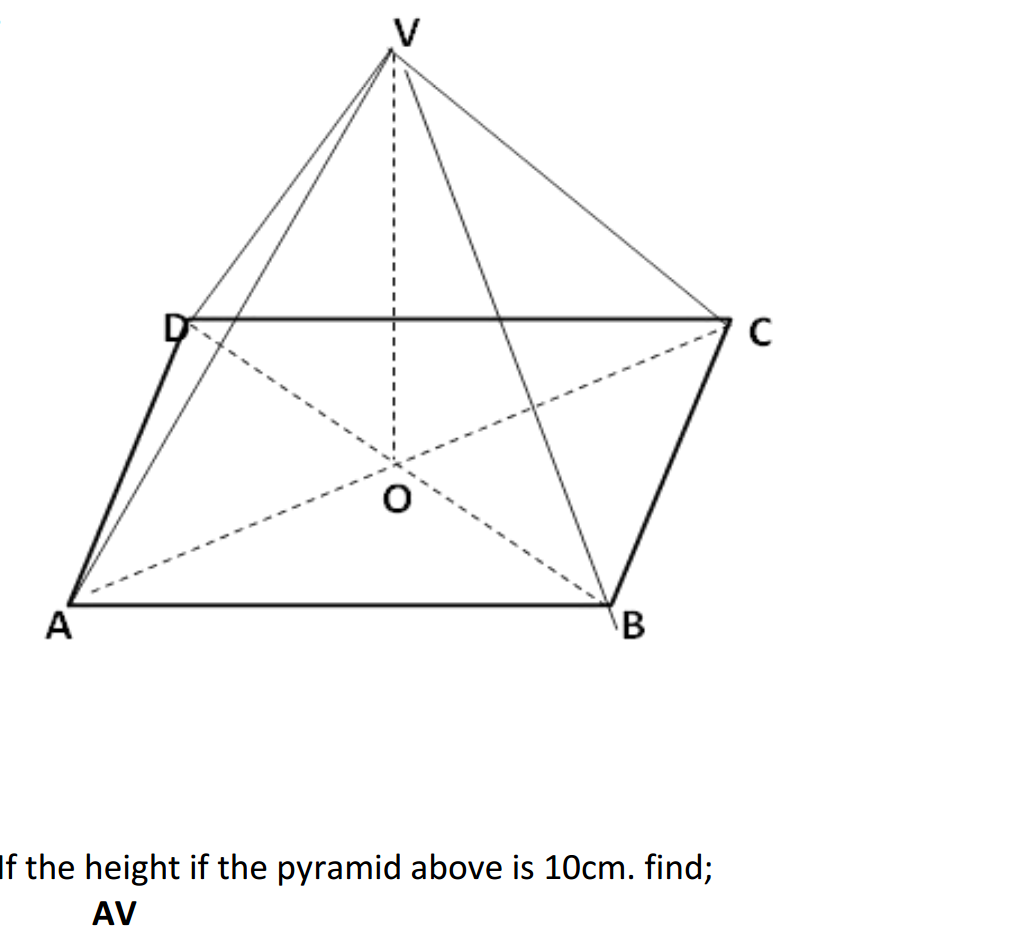
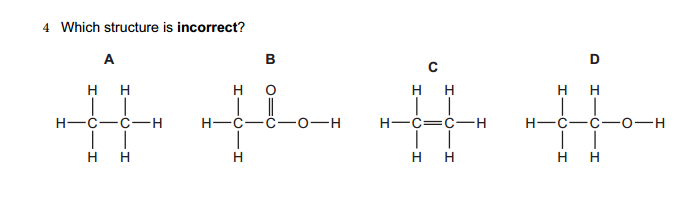
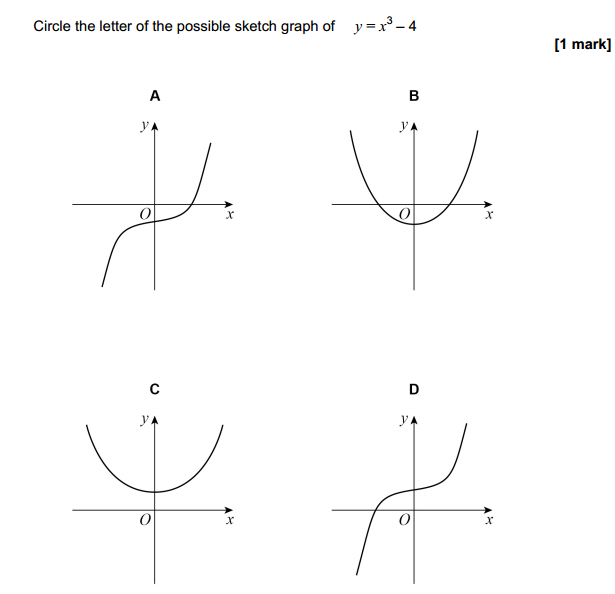
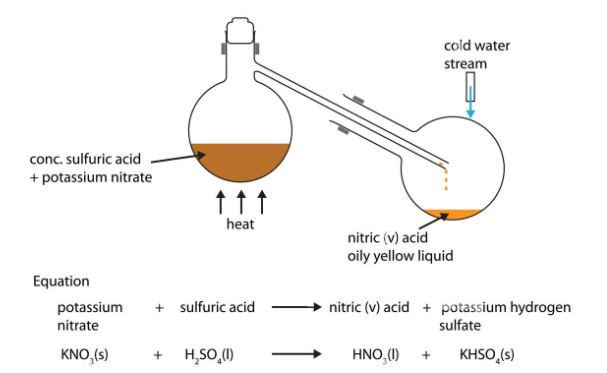
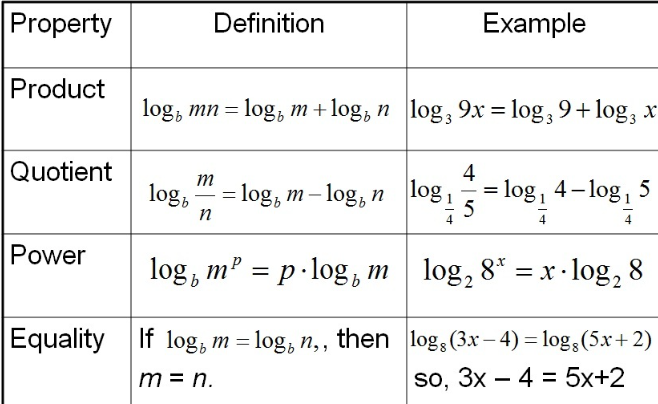
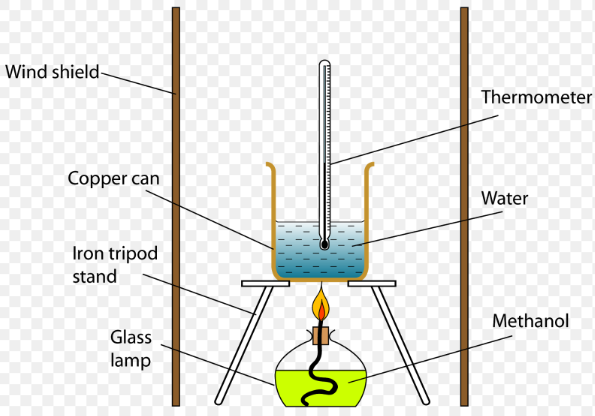
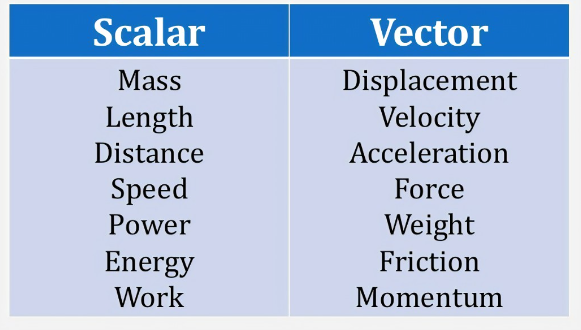
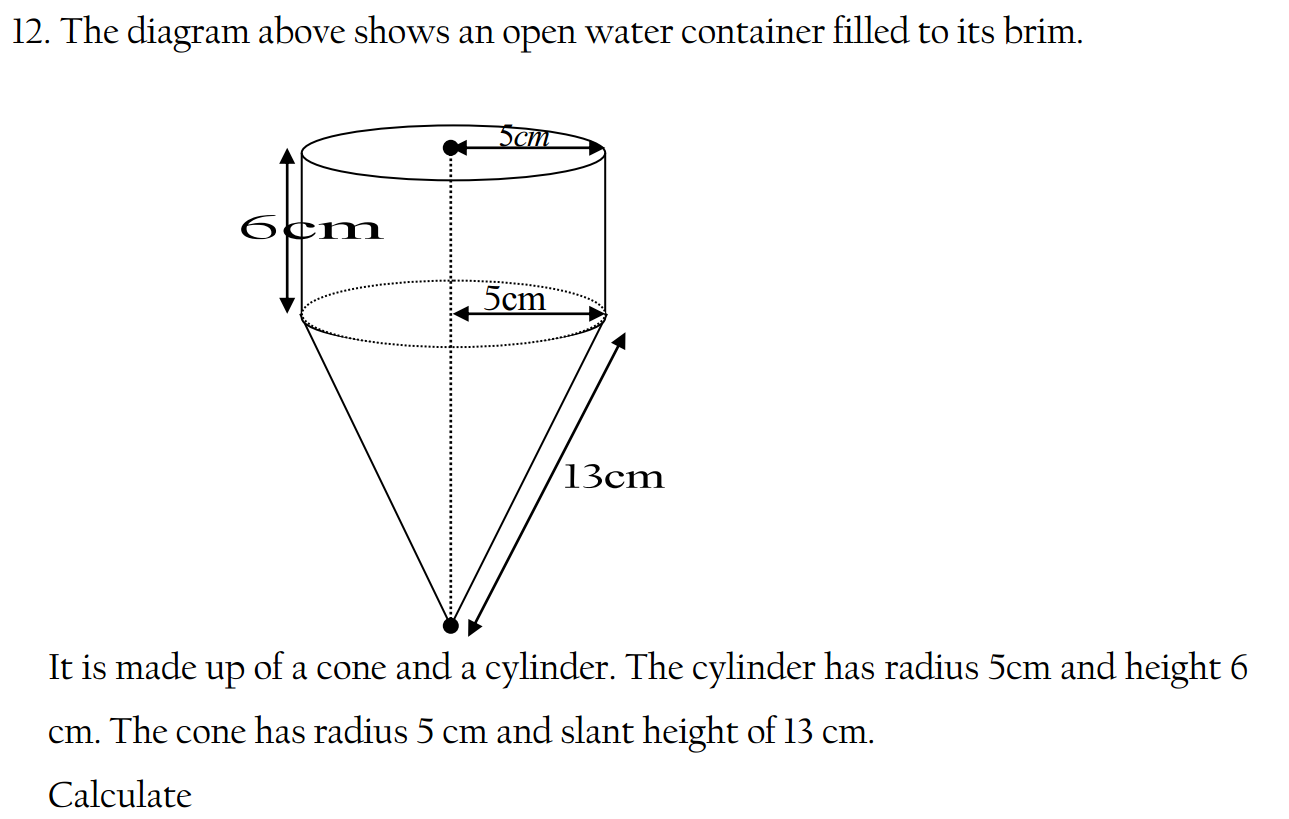
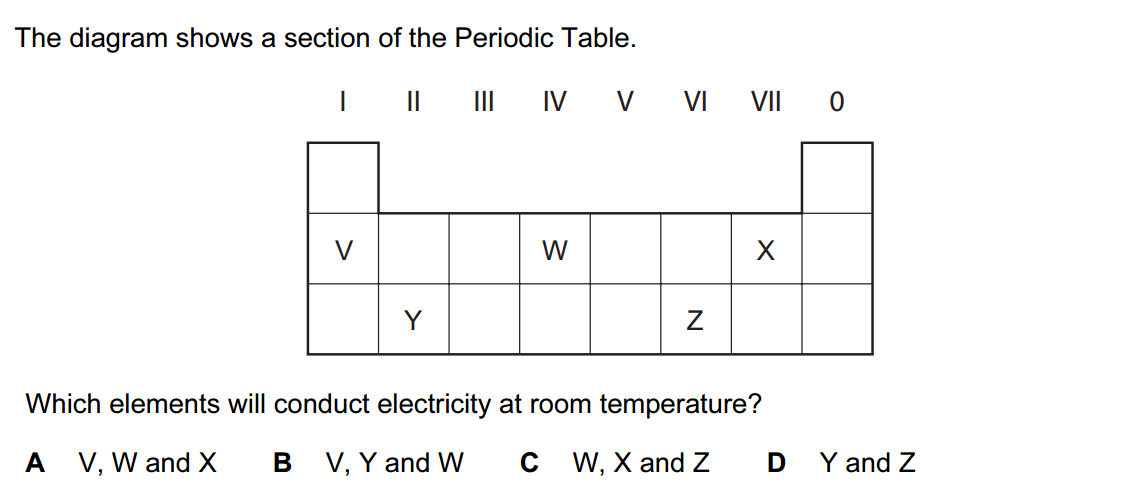
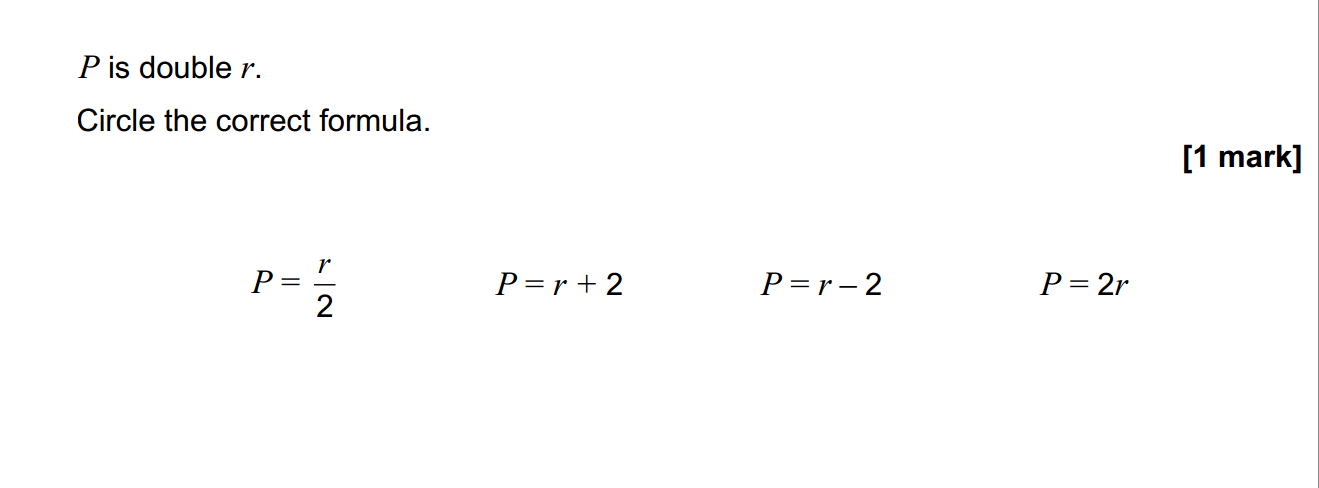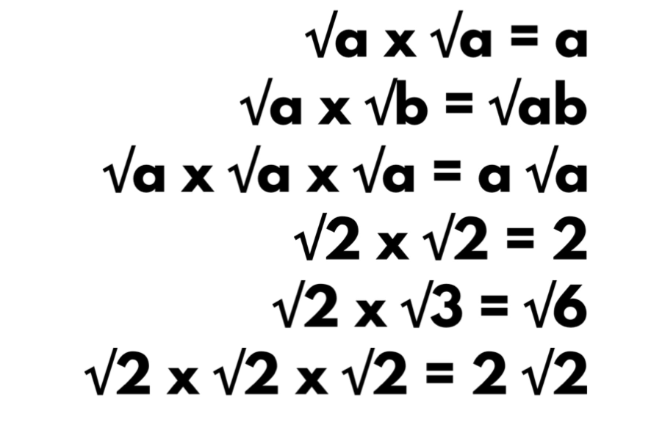1. Define a set and provide an example.
2. What is the cardinality of an empty set?
3. State and explain the concept of the universal set.
4. Explain the concept of a subset and provide an example.
5. What is the difference between a proper subset and an improper subset?
6. State and prove the associative law of set union.
7. Prove De Morgan’s laws for sets: (A ∪ B)’ = A’ ∩ B’ and (A ∩ B)’ = A’ ∪ B’.
8. Explain the concept of the power set and provide an example.
9. State and prove the distributive law of set intersection over set union.
10. Define the complement of a set and provide an example.
11. Prove that the intersection of a set with its complement is the empty set: A ∩ A’ = ∅.
12. State and prove the identity law for set union: A ∪ ∅ = A.
13. Explain the concept of the Cartesian product of sets and provide an example.
14. State and prove the identity law for set intersection: A ∩ U = A.
15. Define the concept of set equality and provide an example.
16. Prove that the union of a set with its complement is the universal set: A ∪ A’ = U.
17. Explain the concept of disjoint sets and provide an example.
18. State and prove the idempotent law for set union: A ∪ A = A.
19. Define the concept of a finite set and provide an example.
20. State and prove the idempotent law for set intersection: A ∩ A = A.

These questions cover various aspects of set theory, including definitions, set operations, set laws, and properties.