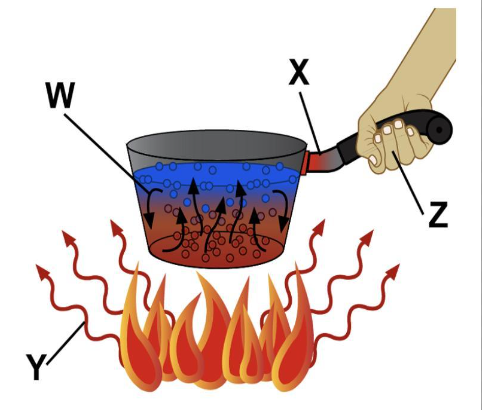
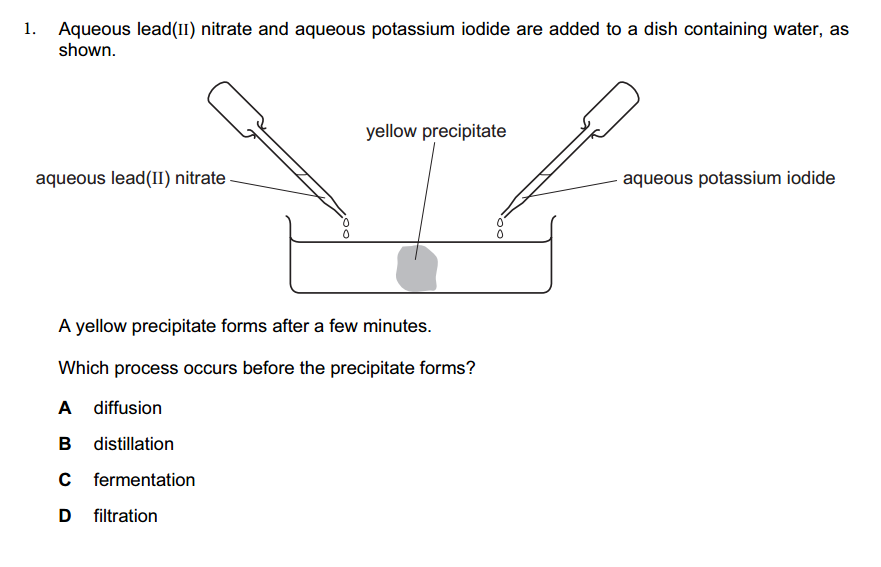
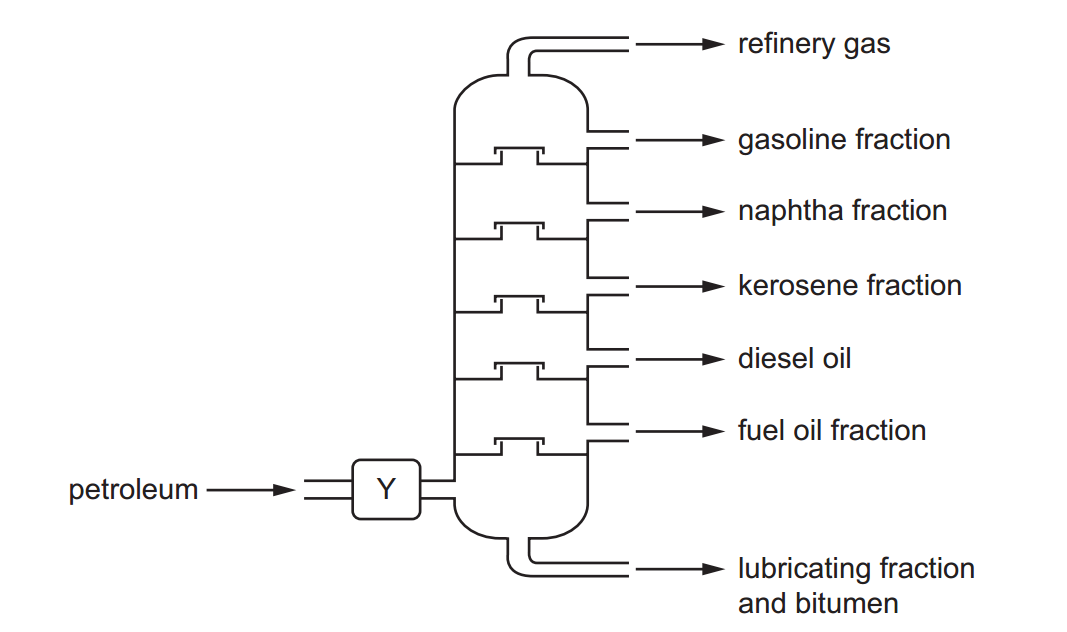
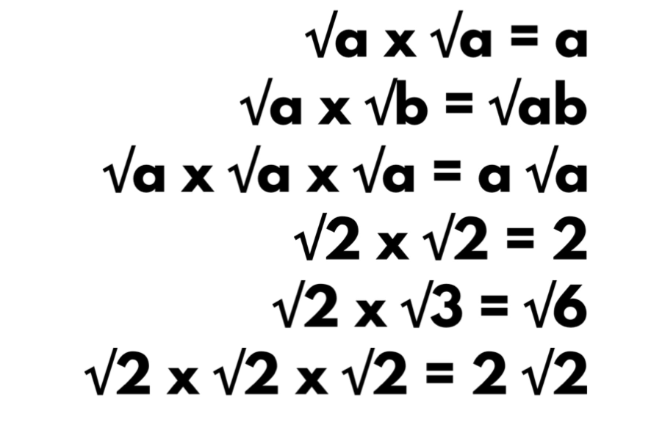Algebra is a fundamental branch of mathematics that deals with symbols, variables, and their relationships, often used to represent quantities without specific values. Its primary focus is on solving equations and manipulating mathematical expressions using operations like addition, subtraction, multiplication, division, and exponentiation.
Here’s a brief overview of what algebra covers and its purpose:
- Variables and Constants: Algebra uses letters (variables like x, y, z) to represent unknown or changing values, and constants (numbers) to represent fixed values.
- Expressions: Algebra involves working with expressions, which are combinations of variables, constants, and mathematical operations. These expressions can be simplified, combined, or evaluated.
- Equations: Equations are statements asserting that two expressions are equal. Algebra helps solve equations to find the values of variables that satisfy the equality.
- Inequalities: Algebra also deals with inequalities, where expressions are compared using symbols like < (less than), > (greater than), ≤ (less than or equal to), or ≥ (greater than or equal to).
- Functions: Functions describe relationships between variables. They take an input (often represented by x) and produce an output (represented by f(x) or y) according to a specific rule or formula.
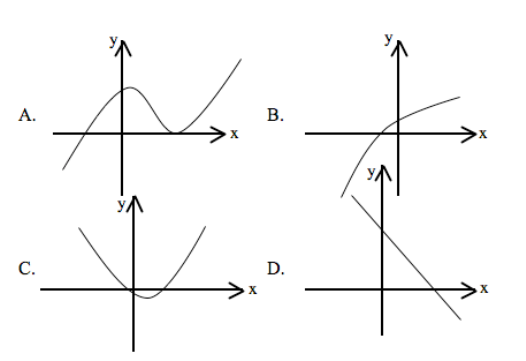
- Graphing: Algebra involves graphing equations and functions on coordinate planes to visually represent relationships between variables.
The purpose of algebra is multifaceted:
- Problem Solving: It provides tools to solve problems in various fields like science, engineering, economics, and more.
- Logical Reasoning: Algebra develops logical thinking and problem-solving skills by breaking down complex problems into simpler steps.
- Modeling Relationships: It helps model and understand relationships between quantities, enabling predictions and analysis.
- Foundation for Advanced Math: Algebra forms the basis for higher-level math concepts like calculus, trigonometry, and linear algebra.
Overall, algebra serves as a powerful tool in understanding, analyzing, and solving a wide range of mathematical problems and real-world situations by abstracting and representing patterns and relationships.
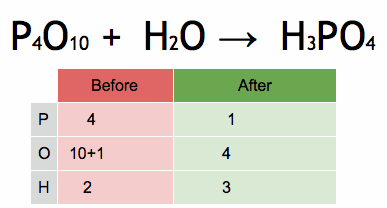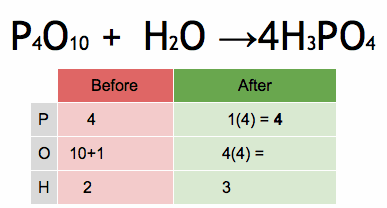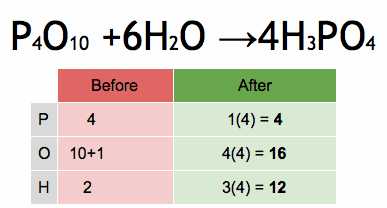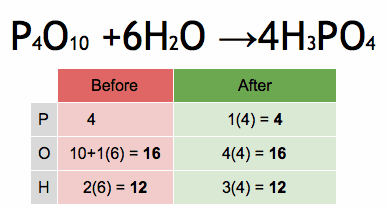
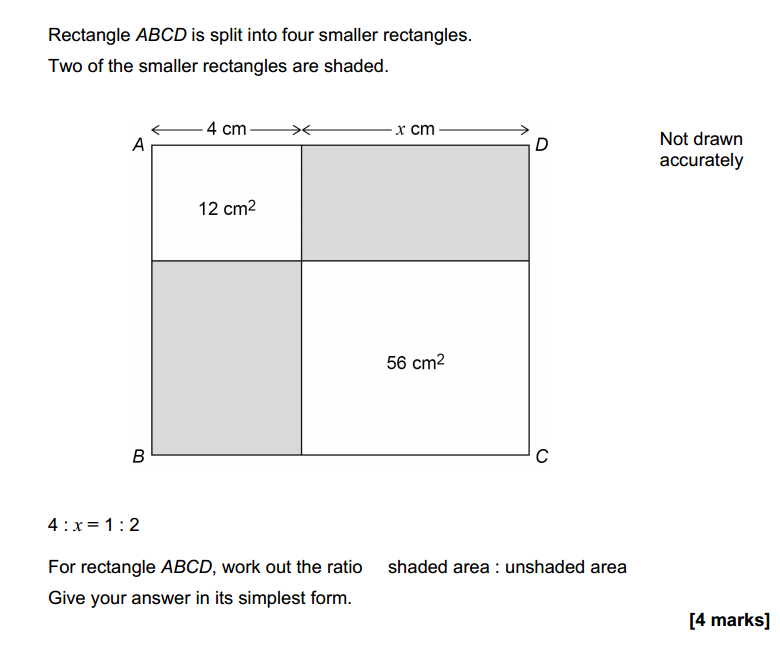
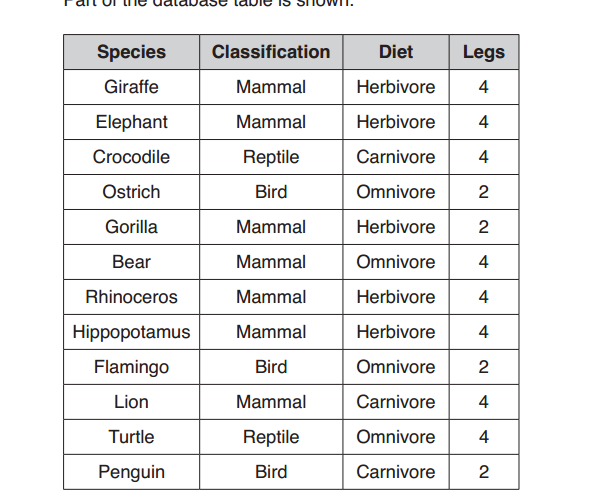
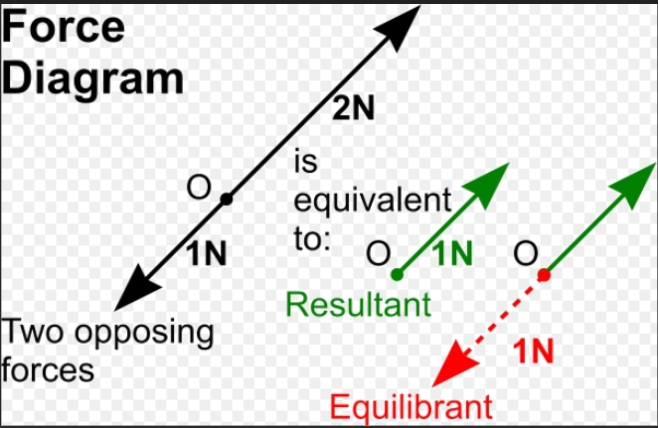
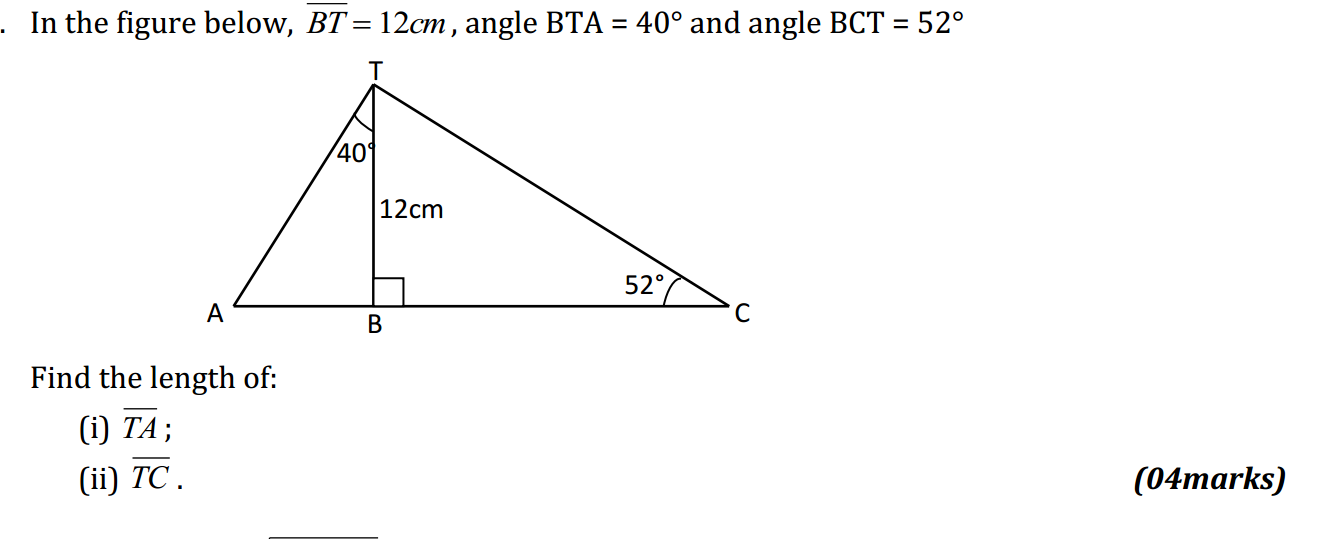
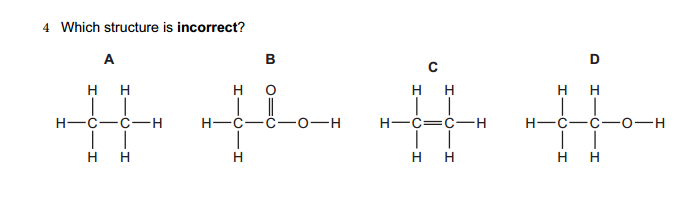
Take a look at these algebraic examples and solve some if you cannot solve all. if you got some answers, you could post them in comment form if you do not mind. You can pause at any slide you want to work on.