Description, Definition and Application of Trigonometry. Math and Physics lovers…

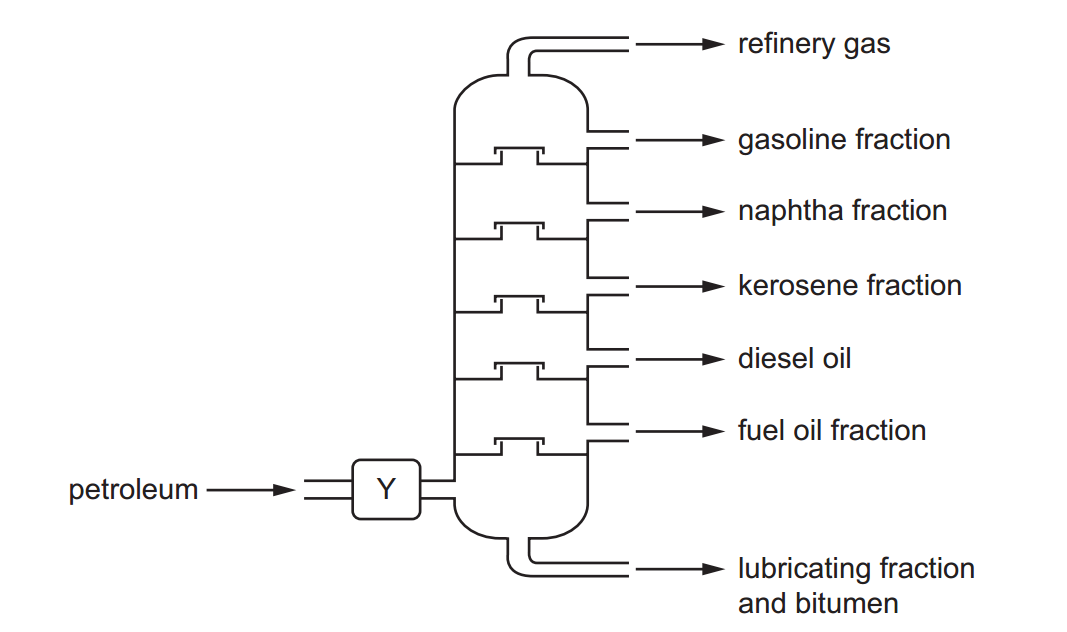
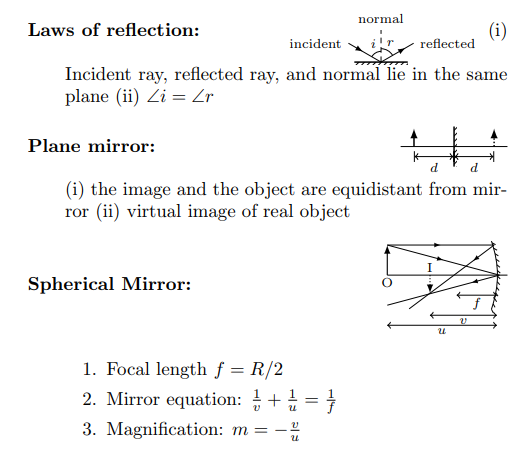
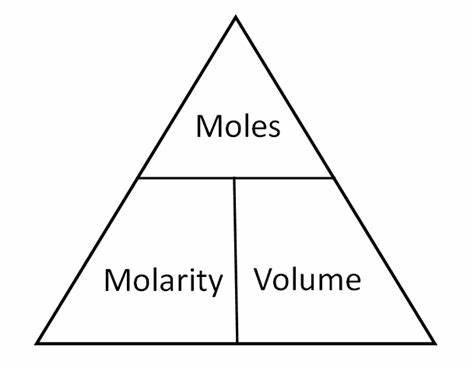
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It has a wide range of applications in various fields, including science, engineering, architecture, and even art. Here are some of the key concepts in trigonometry and their practical applications:

1. Sine, Cosine, and Tangent: These are the fundamental trigonometric functions. They relate the angles of a right triangle to the ratios of its sides.
   • Applications:
     • Navigation: Trigonometry is used in navigation to determine the angles and distances between points on the Earth’s surface. Sailors, pilots, and GPS systems use trigonometric principles to plot courses.
     • Engineering: Engineers use trigonometry to calculate forces and stresses in structures and analyze mechanical systems.
     • Architecture: Architects use trigonometry to design and construct buildings, ensuring they are structurally sound and aesthetically pleasing.
2. Pythagorean Theorem: This theorem relates the lengths of the sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
   • Applications:
     • Construction: The Pythagorean theorem is used in construction to ensure that corners are at right angles and to calculate distances.
     • Physics: It is applied in physics to analyze motion, calculate distances, and solve problems related to vectors and forces.
3. Trigonometric Identities: Trigonometric identities are equations that are true for all values of the variables. Examples include the Pythagorean identities and the sum and difference formulas.
   • Applications:
     • Electrical Engineering: Trigonometric identities are used in the analysis of alternating current (AC) circuits and in signal processing.
     • Robotics: In robotics, trigonometric identities help calculate the position and movement of robot arms and end-effectors.
     • Physics: Trigonometric identities are applied in quantum mechanics and wave mechanics to describe the behavior of particles and waves.
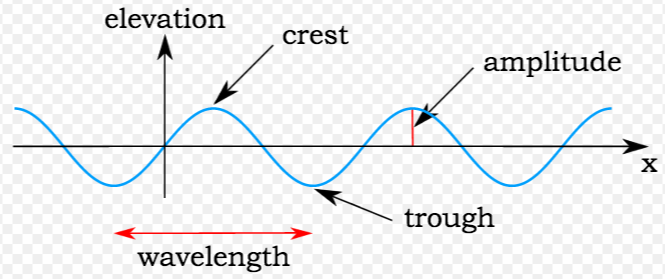
4. Trigonometric Functions and Waves: Sine and cosine functions are used to describe periodic phenomena, such as sound waves and electromagnetic waves.
   • Applications:
     • Music: Trigonometric functions are used to describe and analyze musical tones, including frequency, amplitude, and harmonics.
     • Optics: Sine and cosine functions are used to describe the behavior of light waves, including diffraction and interference.
5. Trigonometric Equations: Trigonometric equations involve solving for unknown angles or sides in various contexts.
   • Applications:
     • Surveying: Trigonometric equations are used to measure distances, heights, and angles in land surveying.
     • Astronomy: Astronomers use trigonometric equations to calculate the positions and distances of celestial objects.
6. Trigonometric Applications in Calculus: Trigonometry is used extensively in calculus, especially when dealing with rates of change and the behavior of functions.
   • Applications:
     • Engineering: Calculus, including trigonometric concepts, is applied in engineering to solve problems related to motion, optimization, and fluid dynamics.
7. Digital Signal Processing (DSP): In DSP, trigonometry plays a vital role in processing and analyzing digital signals, such as audio and video.
   • Applications:
     • Audio Processing: Trigonometry is used to manipulate audio signals, such as filtering, compression, and effects processing.
     • Image Processing: In image processing, trigonometric concepts are employed for tasks like image compression and enhancement.
8. Trigonometry in Game Development: Game developers use trigonometry to create realistic 2D and 3D graphics, simulate physics, and design game mechanics.
   • Applications:
     • Graphics and Animation: Trigonometry is used to calculate angles, distances, and positions of game elements and characters.
     • Physics Simulations: In-game physics engines rely on trigonometry to model object movement and collision detection.

Trigonometry is a versatile mathematical tool with a wide range of practical applications, from everyday tasks like navigation to highly specialized fields like particle physics and game development. Its concepts are fundamental to understanding and solving complex problems in various scientific and engineering domains.