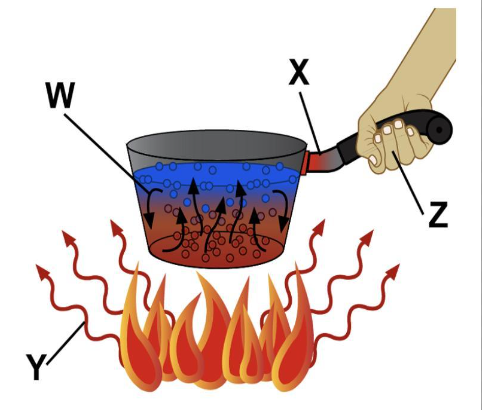
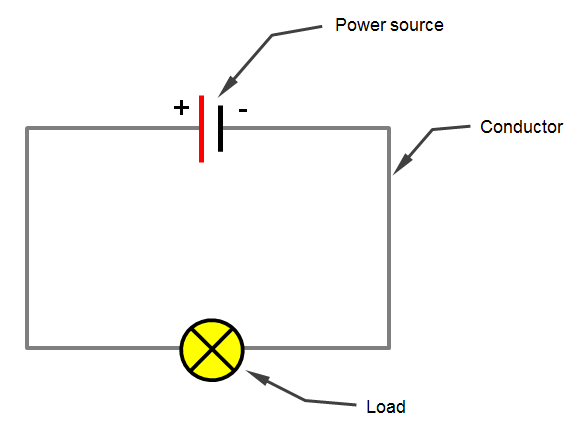
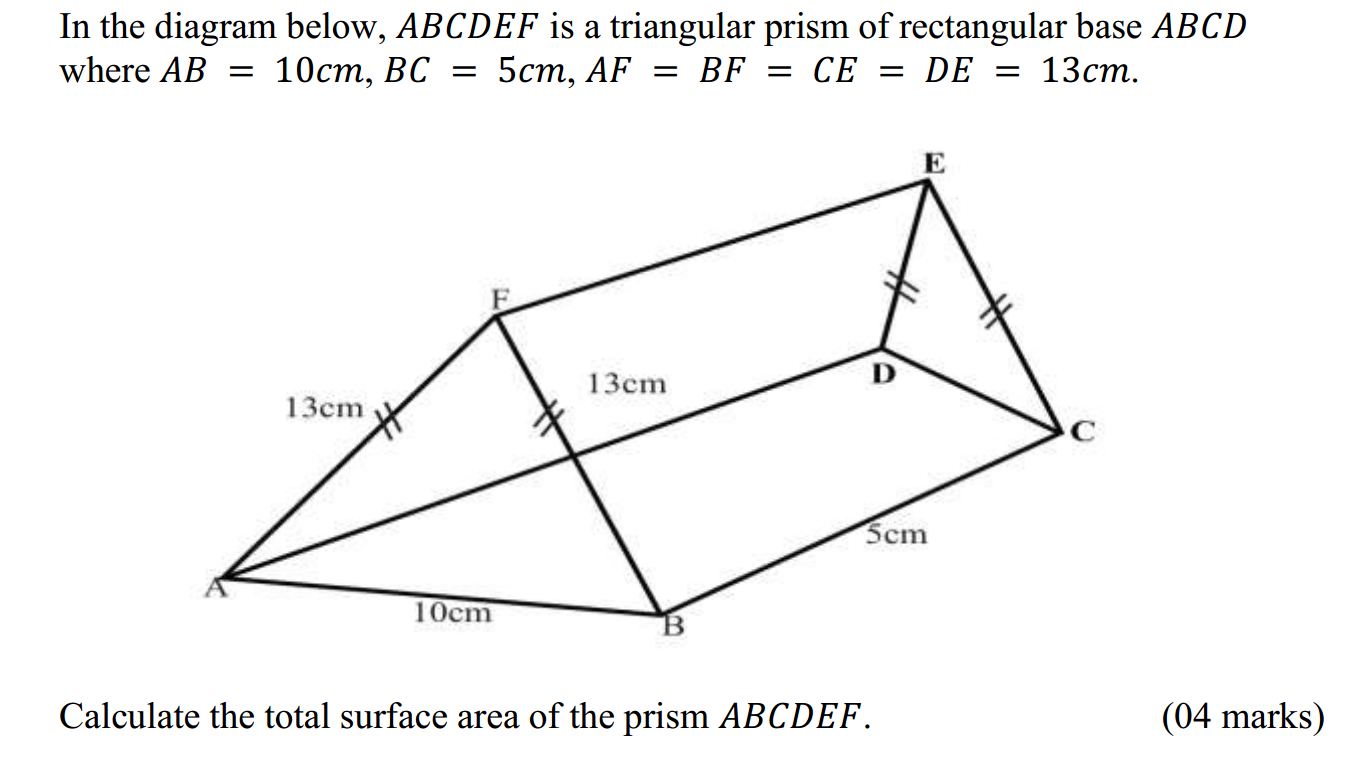
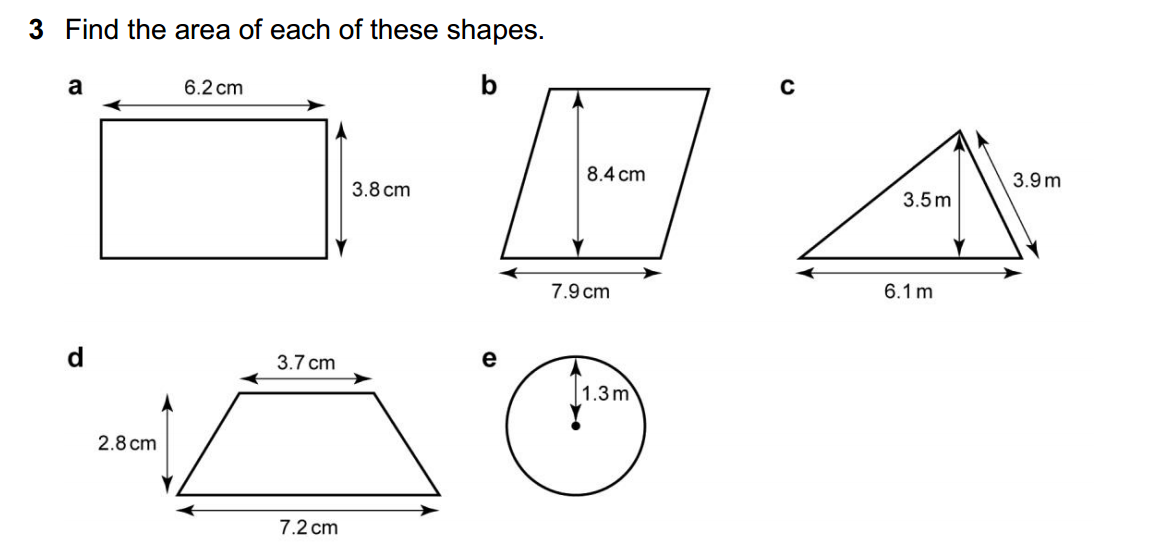
Mathematics is often referred to as the language of the universe. Its principles and concepts form the foundation upon which the physical sciences are built. From physics and chemistry to astronomy and geology, mathematical equations and models are essential for understanding and describing the natural world. In this blog post, we will explore why mathematics is considered the backbone of physical sciences and how it plays a crucial role in scientific discoveries and advancements.
The Fundamental Role of Mathematics in Physical Sciences
- Quantitative Analysis
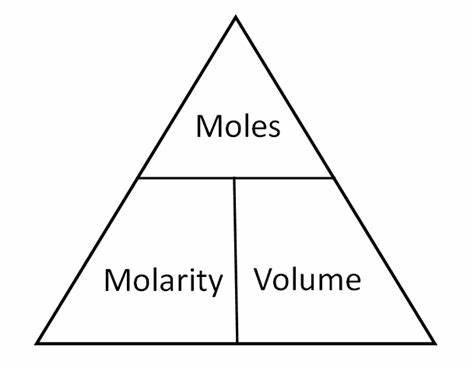
- Mathematics allows scientists to quantify observations and phenomena. This quantitative analysis is crucial for measuring, comparing, and predicting outcomes in physical sciences.
- For example, in physics, mathematical formulas such as Newton’s laws of motion describe the relationship between forces and the motion of objects.
- Precision and Accuracy
- Mathematical models provide a precise and accurate way to represent physical phenomena. These models can be tested and refined to improve their accuracy.
- In chemistry, the use of mathematical equations, like the ideal gas law, enables scientists to predict the behavior of gases under different conditions with high precision.
- Prediction and Hypothesis Testing
- Mathematics enables scientists to make predictions about the behavior of systems and test hypotheses through experiments.
- In astronomy, mathematical models of planetary motion allow astronomers to predict celestial events, such as eclipses and the positions of planets.
- Unifying Principles
- Mathematics provides a unifying framework that can connect different physical phenomena through common principles.
- The concept of energy, for example, is unified through mathematical equations in various fields, from kinetic energy in mechanics to thermal energy in thermodynamics.
- Complex Systems and Simulations
- Advanced mathematical techniques, such as differential equations and linear algebra, are used to model and simulate complex systems that are difficult to study experimentally.
- In climate science, mathematical models are essential for simulating weather patterns and predicting climate change.
Examples of Mathematics in Physical Sciences
- Physics
- Mechanics: Newton’s laws of motion, expressed as mathematical equations, describe how objects move and interact.
- Electromagnetism: Maxwell’s equations use vector calculus to describe how electric and magnetic fields propagate and interact.
- Chemistry
- Stoichiometry: Mathematical calculations determine the proportions of reactants and products in chemical reactions.
- Quantum Chemistry: Schrödinger’s equation uses differential equations to describe the behavior of electrons in atoms and molecules.
- Astronomy
- Orbital Mechanics: Kepler’s laws of planetary motion and Newton’s law of gravitation use mathematical equations to describe the orbits of celestial bodies.
- Astrophysics: Mathematical models describe the structure and evolution of stars, galaxies, and the universe.
- Geology
- Seismology: Mathematical models of wave propagation help scientists understand and predict the behavior of seismic waves during earthquakes.
- Plate Tectonics: Geometry and vector calculus describe the movement and interaction of Earth’s tectonic plates.
The Interplay Between Mathematics and Physical Sciences
Mathematics and physical sciences have a symbiotic relationship. While mathematics provides the tools and frameworks needed to understand and describe physical phenomena, discoveries in physical sciences often lead to the development of new mathematical theories and techniques. This interplay has driven scientific progress for centuries and continues to do so today.
- Historical Examples:
- Isaac Newton’s development of calculus was motivated by his work on the laws of motion and gravitation.
- Albert Einstein’s theory of relativity required the use of non-Euclidean geometry and advanced mathematical concepts.
- Modern Examples:
- The study of chaos theory and nonlinear dynamics has been driven by the need to understand complex systems in physics and other sciences.
- The development of computational mathematics has revolutionized fields like materials science, allowing for the simulation and discovery of new materials with desirable properties.
Conclusion
Mathematics is undeniably the backbone of physical sciences. Its ability to provide precise, accurate, and unifying descriptions of natural phenomena makes it an indispensable tool for scientists. As we continue to explore the mysteries of the universe, mathematics will remain at the core of our quest for knowledge, driving scientific discovery and innovation.
Whether you are a student, educator, or enthusiast, appreciating the role of mathematics in physical sciences can deepen your understanding and inspire you to explore the wonders of the natural world.