Understanding Surds and Squares: Essential Concepts in Mathematics

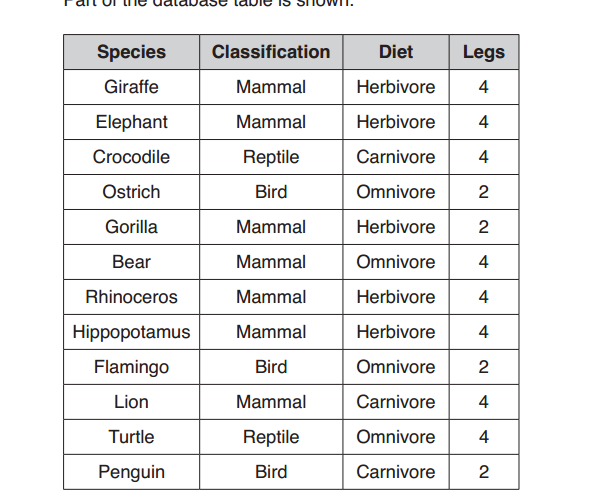
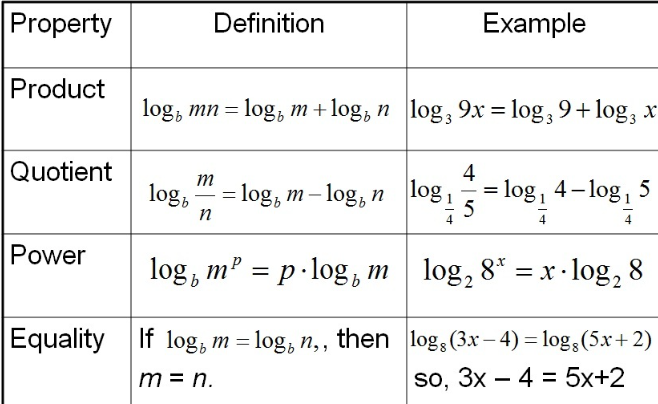
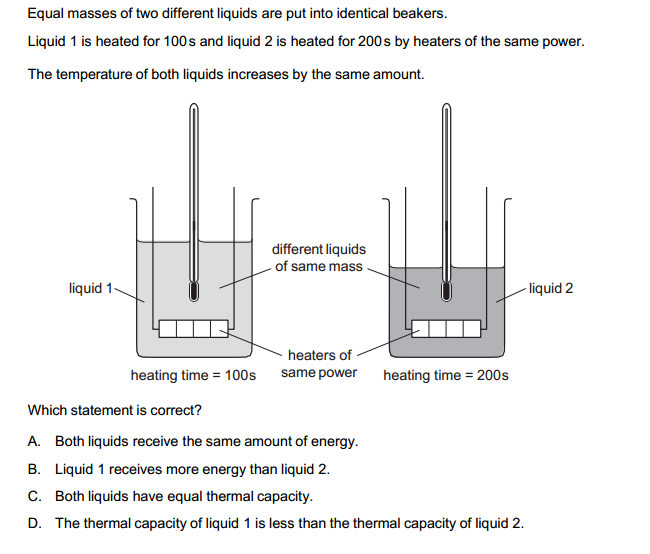
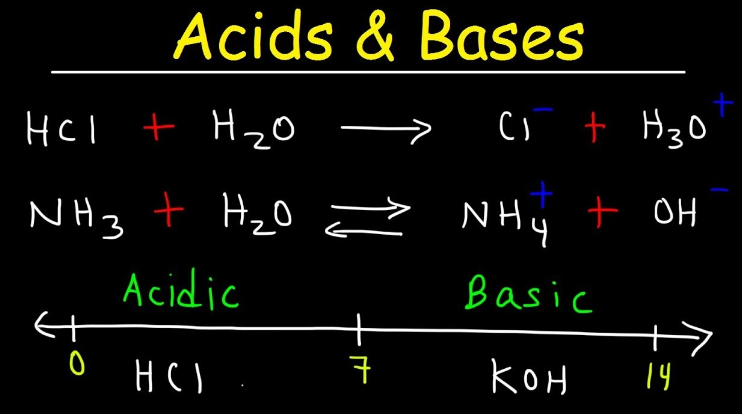
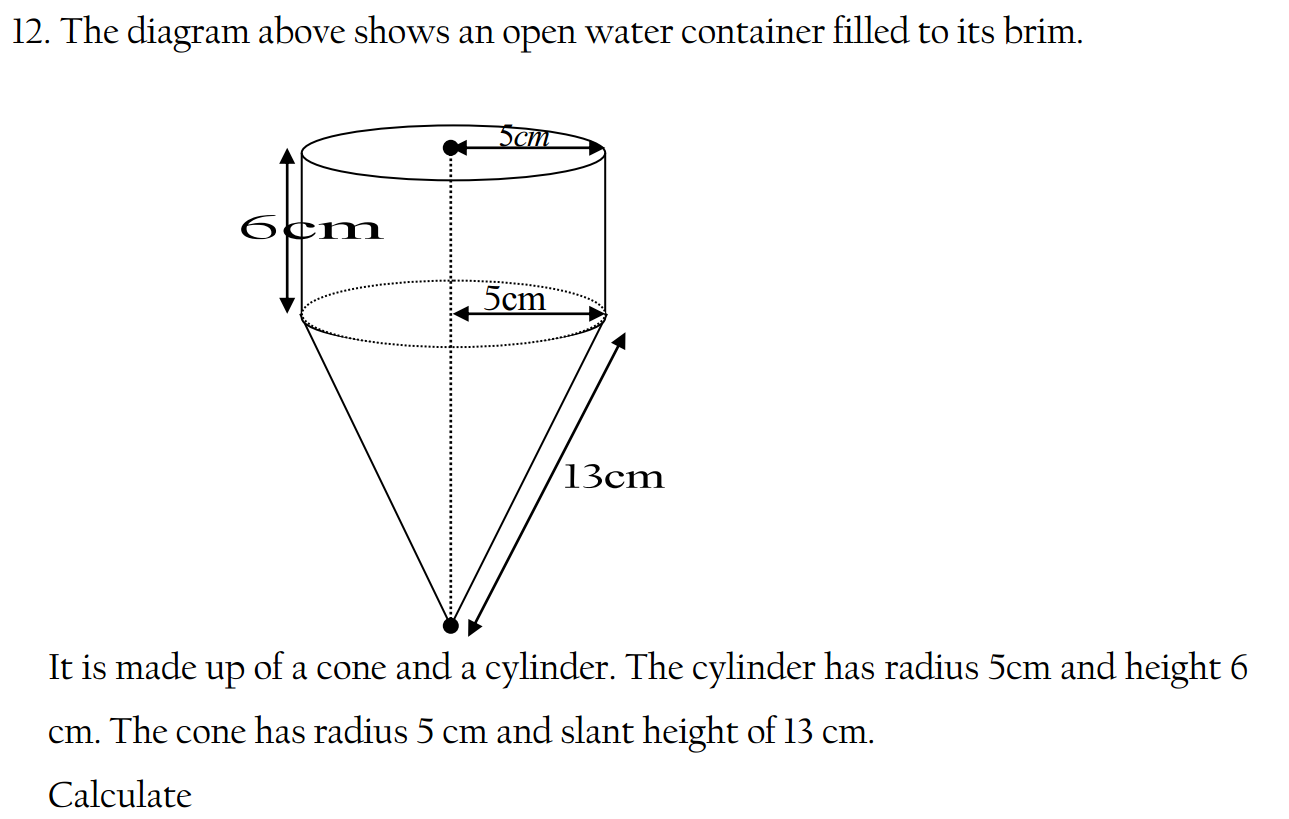
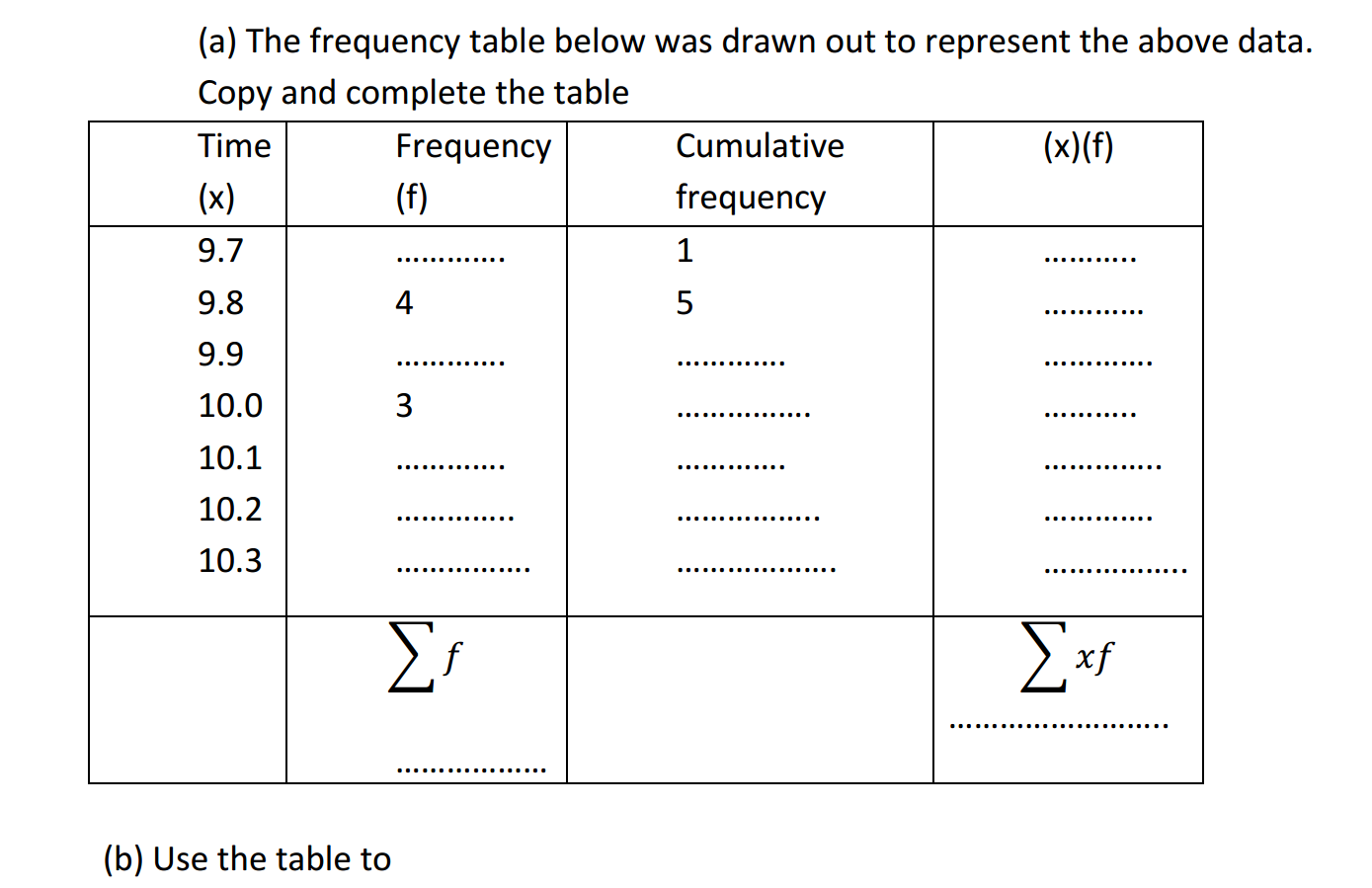
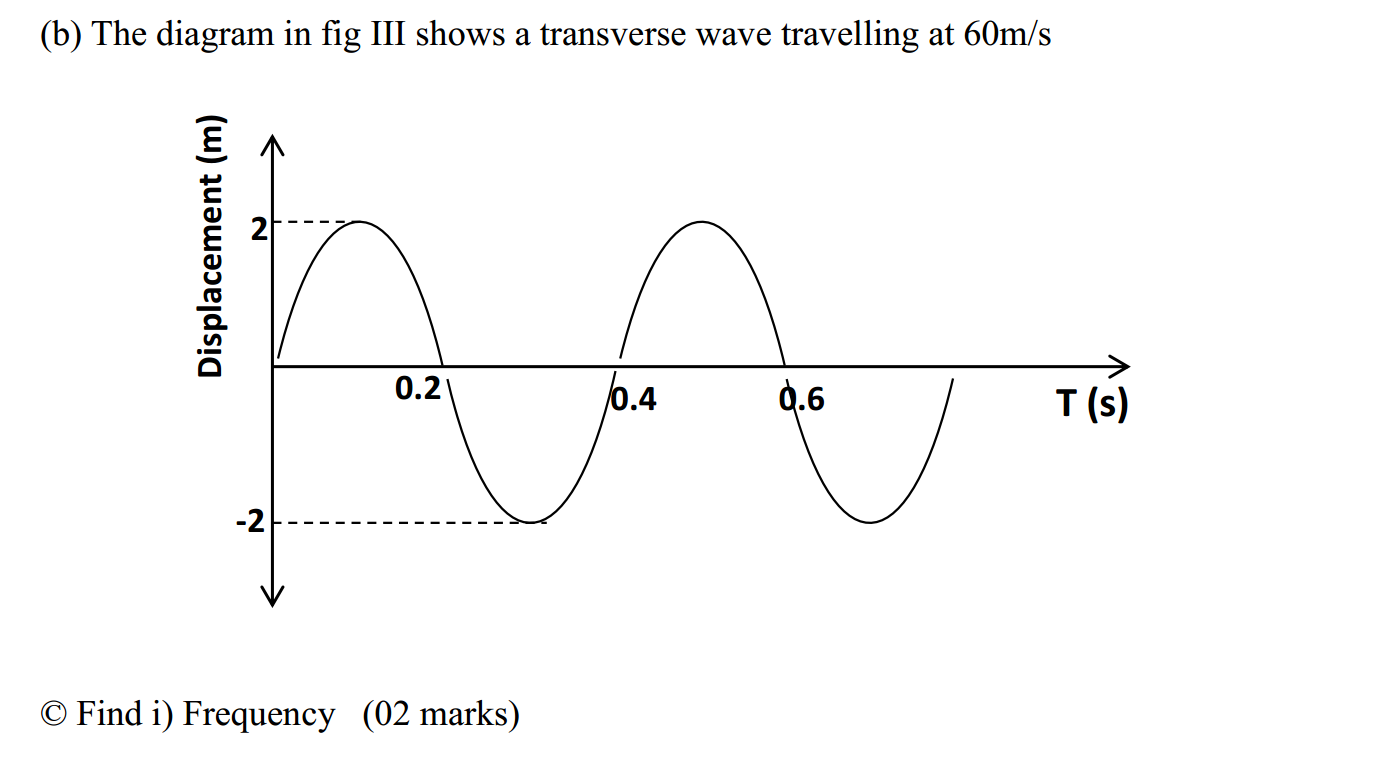
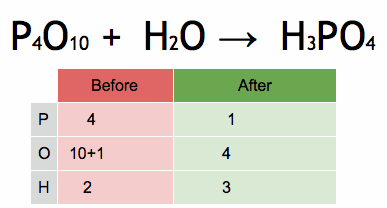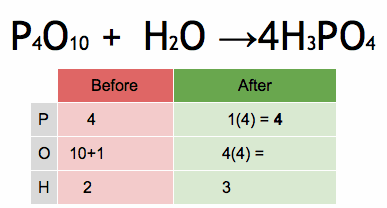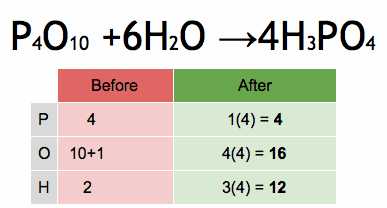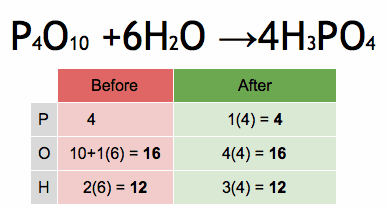
Surds and squares are fundamental concepts in mathematics, particularly in the realm of algebra and arithmetic. Let’s explore each of these concepts individually and then see how they relate to each other.

Surds:

A surd is an irrational number that cannot be expressed as the quotient of two integers. In simpler terms, it’s a number that cannot be written as a finite, non-repeating decimal. Surds often arise when taking the square root of a non-perfect square or when dealing with certain geometric problems.

Examples of Surds:

1. √2 (Square root of 2)
2. √3 (Square root of 3)
3. √5 (Square root of 5)

Squares:

A square is a number multiplied by itself. For example, 4 is a square because it can be expressed as 2 × 2, and 9 is a square because it can be expressed as 3 × 3. The term “square” comes from the geometric shape, a square, which has four equal sides.

Examples of Squares:

1. 1 (1 × 1)
2. 4 (2 × 2)
3. 9 (3 × 3)
4. 16 (4 × 4)

Relationship Between Surds and Squares:

Surds and squares are related through the process of taking square roots. When we take the square root of a perfect square (a number that can be expressed as the square of an integer), we get a rational number. However, when we take the square root of a non-perfect square (a number that cannot be expressed as the square of an integer), we get a surd.

For example:

• The square root of 4 is 2, which is a rational number.
• The square root of 2 is √2, which is a surd.

Operations with Surds and Squares:

When dealing with surds and squares, it’s essential to understand how to perform operations such as addition, subtraction, multiplication, and division. These operations follow specific rules and properties, such as:

1. Addition and Subtraction: Surds with the same irrational part can be added or subtracted, but surds with different irrational parts cannot be combined.
2. Multiplication: To multiply surds, you simply multiply the numbers outside the square root (known as the coefficients) and multiply the numbers inside the square root together.
3. Division: To divide surds, divide the numbers outside the square root and divide the numbers inside the square root.

Understanding surds and squares is crucial in various mathematical contexts, including algebraic simplification, solving equations, and geometry. Mastery of these concepts allows mathematicians to manipulate and analyze expressions involving irrational numbers efficiently.